Порівняння дробів: основи, які відкривають двері до математики
Дроби — це не просто числа з рискою посередині, а справжні ключі до розуміння пропорцій, часток і навіть нашого повсякденного життя. Від приготування пирога за рецептом до підрахунку знижок у магазині — вміння порівнювати дроби рятує нас у найнесподіваніших ситуаціях. У цьому матеріалі ми розберемо, як порівнювати дроби крок за кроком, зануримося в нюанси, які часто залишаються поза увагою, і зробимо це так, щоб навіть новачок відчув себе впевненим математиком.
Що таке дріб і чому важливо вміти їх порівнювати?
Дріб — це спосіб виразити частину цілого. Наприклад, якщо ви розрізаєте піцу на 8 шматків і берете 3, то ваша частка — це 3/8. Порівняння дробів допомагає зрозуміти, яка частка більша чи менша, що критично важливо для багатьох задач. Чи буде 3/8 піци достатньо, щоб нагодувати друга, чи краще взяти 5/12? Щоб відповісти, потрібно знати, як ці числа співвідносяться.
Порівняння дробів — це не лише про математику в зошиті. Це про рішення, які ми приймаємо щодня. І хоча на перший погляд здається, що все просто, є підводні камені, які можуть збити з пантелику. Давайте розбиратися, як уникнути плутанини і зробити процес зрозумілим.
Основні методи порівняння дробів
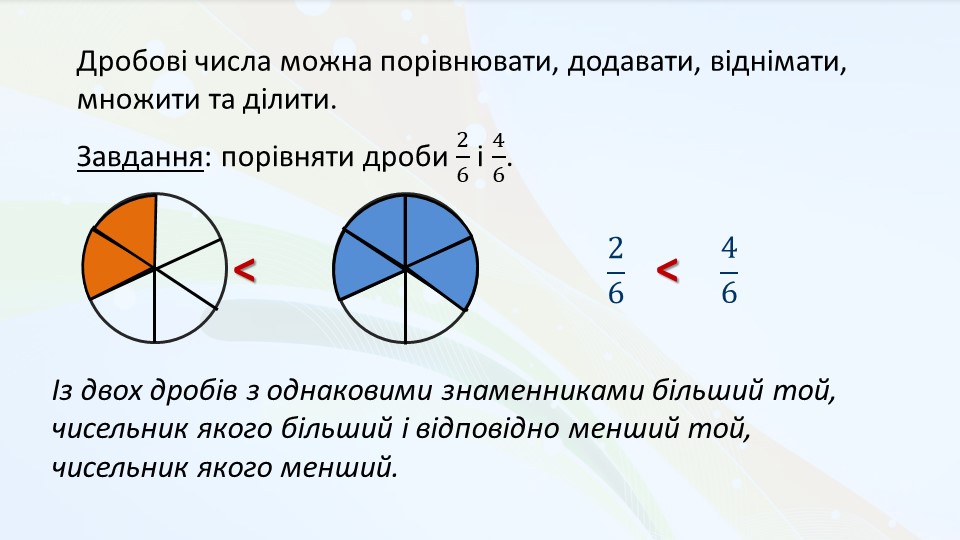
Порівняння дробів із однаковими знаменниками
Найпростіший випадок — коли дроби мають однаковий знаменник, тобто нижня частина дробу збігається. Тут усе зводиться до порівняння чисельників (верхньої частини). Більший чисельник означає більший дріб. Наприклад, у дробах 2/5 і 3/5 більшим буде 3/5, адже 3 більше за 2.
Це як порівняння шматків торта, розрізаного на однакові частини. Якщо торт поділений на 5 шматків, то 3 шматки завжди будуть більше, ніж 2. Логічно, чи не так? Але цей метод працює лише для однакових знаменників, інакше потрібен інший підхід.
Приведення до спільного знаменника
Коли знаменники різні, порівняння стає трохи складнішим, але не менш цікавим. Уявіть, що ви порівнюєте шматки двох різних тортів: один розрізаний на 4 частини, а інший — на 6. Як зрозуміти, що більше — 1/4 чи 2/6? Для цього потрібно привести дроби до спільного знаменника, тобто зробити так, щоб нижня частина обох дробів була однаковою.
Процес виглядає так: знаходите найменше спільне кратне (НСК) для знаменників. Для 4 і 6 це буде 12. Потім перетворюєте кожен дріб, щоб знаменник став 12. Для 1/4: множимо чисельник і знаменник на 3, отримуємо 3/12. Для 2/6: множимо на 2, отримуємо 4/12. Тепер порівнюємо чисельники — 3 і 4. Очевидно, що 4/12 (тобто 2/6) більше, ніж 3/12 (тобто 1/4).
Цей метод — справжній рятівник, коли дроби виглядають зовсім різними. Але не поспішайте, адже важливо правильно підібрати НСК, щоб не ускладнювати обчислення. А тепер давайте подивимося, чи є швидший спосіб для деяких випадків.
Порівняння через десяткові дроби
Іноді простіше перетворити дроби на десяткові числа, особливо якщо знаменники великі чи незручні для обчислень. Наприклад, порівняємо 5/8 і 3/5. Ділимо чисельник на знаменник: 5 ÷ 8 = 0.625, а 3 ÷ 5 = 0.6. Очевидно, що 0.625 більше за 0.6, тобто 5/8 більше за 3/5.
Цей спосіб зручний, коли ви маєте калькулятор під рукою або коли дроби легко переводяться в десяткові. Але будьте обережні: іноді десяткові значення можуть бути нескінченними (як у випадку з 1/3 = 0.333…), і порівняння може стати менш точним, якщо округлити числа.
Метод “перехресного множення”
Є ще один елегантний спосіб, який економить час, — перехресне множення. Він працює для дробів із різними знаменниками і дозволяє уникнути приведення до спільного знаменника. Візьмемо дроби 3/7 і 2/5. Множимо чисельник першого дробу на знаменник другого: 3 × 5 = 15. Потім чисельник другого на знаменник першого: 2 × 7 = 14. Порівнюємо результати: 15 більше за 14, отже, 3/7 більше за 2/5.
Цей метод схожий на швидкий трюк фокусника: кілька рухів — і відповідь готова. Але пам’ятайте, що він працює лише для порівняння двох дробів і не підходить, якщо потрібно впорядкувати більше чисел.
Порівняння дробів із цілими числами та змішаними числами
Дроби та цілі числа
Порівняння дробів із цілими числами здається простим, але іноді може здивувати. Наприклад, 7/4 більше за 1, адже 7/4 дорівнює 1 і 3/4. Щоб порівняти, перетворіть ціле число в дріб із тим самим знаменником: 1 = 4/4. Тепер видно, що 7/4 більше за 4/4.
Це як порівняння повного кошика яблук із частковим. Якщо у вас є кошик і ще кілька яблук зверху, це явно більше, ніж просто один кошик. Такі порівняння допомагають зрозуміти, як дроби вписуються в ширшу картину чисел.
Змішані числа: як розібратися?
Змішані числа — це комбінація цілого числа та дробу, наприклад, 2 1/3. Щоб порівняти їх із звичайними дробами, спочатку перетворіть змішане число в неправильний дріб. Для 2 1/3 це буде (2 × 3 + 1)/3 = 7/3. Тепер порівняння з іншим дробом, скажімо 5/2, стає стандартним завданням: приводимо до спільного знаменника або використовуємо перехресне множення.
Змішані числа часто зустрічаються в реальному житті. Наприклад, коли ви міряєте відстань чи час, і цей метод дозволяє швидко розібратися, що більше: 2 1/3 години чи 9/4 години. Точність тут — ваш найкращий союзник.
Практичні приклади з життя
Дроби оточують нас усюди, навіть якщо ми цього не помічаємо. Скажімо, ви готуєте вечерю і в рецепті вказано 2/3 склянки цукру, а у вас є лише мірна ложка на 3/4. Чи вистачить того, що є? Порівняння показує: 3/4 більше за 2/3 (приведення до спільного знаменника 12 дає 9/12 проти 8/12), тож у вас навіть залишиться трохи цукру.
Або ж уявіть, що ви обираєте між двома знижками в магазині: одна пропонує 1/5 від ціни, інша — 1/4. Інтуїція може підказати, що 1/4 більший, і порівняння це підтверджує. Такі маленькі математичні перемоги роблять життя простішим і економлять ваші гроші.
Типові помилки при порівнянні дробів
Найпоширеніші помилки
Порівняння дробів здається простим, але навіть досвідчені люди можуть оступитися. Ось кілька пасток, у які легко потрапити, і як їх уникнути.
- 😕 Порівняння лише чисельників чи знаменників. Багато хто думає, що більший чисельник автоматично означає більший дріб. Але це помилка! Наприклад, 3/8 менший за 2/5, хоча 3 більше за 2. Завжди враховуйте обидві частини дробу.
- 🤔 Неправильний вибір спільного знаменника. Іноді люди обирають занадто велике число замість найменшого спільного кратного, що ускладнює обчислення. Для 1/6 і 1/9 НСК — це 18, а не 36 чи 54.
- 😟 Плутанина зі знаком нерівності. Після порівняння легко переплутати, який дріб більший, особливо якщо ви працюєте з кількома числами. Перевіряйте результат ще раз, щоб уникнути дурних помилок.
Ці помилки — не вирок, а просто нагадування, що математика любить увагу до деталей. Тренуйтеся, і з часом ці пастки перестануть бути загрозою.
Порівняння дробів у таблиці: наочний приклад
Щоб усе стало ще зрозумілішим, давайте порівняємо кілька дробів за різними методами в таблиці. Це допоможе побачити, як працюють різні підходи на практиці.
| Дроби | Спільний знаменник | Десяткові значення | Результат порівняння |
|---|---|---|---|
| 1/3 і 2/5 | 5/15 і 6/15 | 0.333 і 0.4 | 2/5 більше за 1/3 |
| 3/8 і 1/2 | 3/8 і 4/8 | 0.375 і 0.5 | 1/2 більше за 3/8 |
Ця таблиця показує, як різні методи дають однаковий результат, якщо все зроблено правильно. Використовуйте той спосіб, який вам зручніший, але завжди перевіряйте свої обчислення. Дані для прикладу взяті з базових математичних принципів, які можна знайти в будь-якому підручнику.
Як тренуватися і вдосконалювати навички?
Порівняння дробів — це навичка, яка приходить із практикою. Почніть із простих дробів, де знаменники однакові, і поступово переходьте до складніших прикладів зі змішаними числами. Використовуйте онлайн-тренажери або спеціальні додатки, які генерують випадкові завдання, щоб відточити свої вміння.
Ще один спосіб — прив’язувати математику до реального життя. Наступного разу, коли будете ділити щось із друзями чи розраховувати пропорції, спробуйте порівняти дроби в голові. Це не лише корисно, а й додає впевненості. А якщо щось не виходить, не хвилюйтеся — навіть маленькі помилки вчать нас більше, ніж ідеальні відповіді.
Математика — це не про те, щоб бути ідеальним, а про те, щоб знаходити шлях до правильної відповіді, навіть якщо він звивистий.
Тож беріть зошит, калькулятор чи просто уявний пиріг, який потрібно поділити, і починайте експериментувати. Дроби — це не нудні числа, а маленькі історії про те, як ціле ділиться на частини. І кожна така історія варта того, щоб її розгадати.