Що таке діагональ: базове розуміння з глибиною
Діагональ простягається через простір фігури, з’єднуючи кути, що не торкаються однієї сторони, ніби невидима стріла, яка пронизує серце геометричного світу. Уявіть квадратний стіл, де від одного кута до протилежного тягнеться пряма лінія – це і є діагональ, що розкриває приховані зв’язки в формах. Вона не просто лінія, а ключ до розрахунків, від будівництва мостів до дизайну екранів смартфонів, де її довжина визначає, наскільки комфортно дивитися відео.
Термін походить з грецької, де “dia” означає “через”, а “gonia” – “кут”, тож діагональ буквально пронизує кути наскрізь. У повсякденному житті ми стикаємося з нею щодня: від телевізорів, де розмір екрану вимірюється саме по діагоналі, до спортивних полів, де вона впливає на стратегію гри. А в математиці діагональ стає інструментом для розв’язання задач, що здаються складними на перший погляд, але розкриваються з елегантною простотою.
Ця концепція еволюціонувала від античних геометрів, як Евклід, які використовували її для доказів теорем, до сучасних інженерів, що застосовують у комп’ютерній графіці. Діагональ не стоїть на місці – вона рухається з часом, адаптуючись до нових технологій, і саме це робить її вічною в нашому світі форм і чисел.
Діагональ у геометричних фігурах: від простих до складних
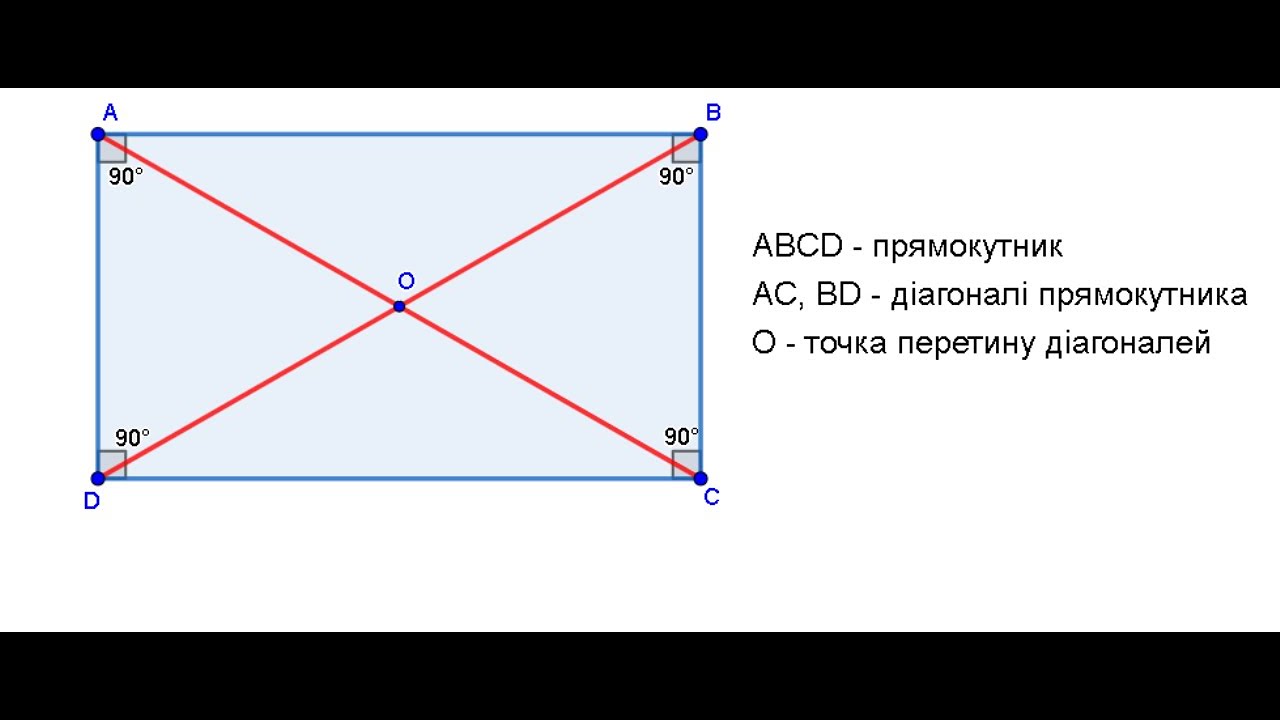
У чотирикутниках діагональ з’єднує несуміжні вершини, створюючи внутрішній місток, що розділяє фігуру на трикутники. Наприклад, у квадраті дві діагоналі перетинаються під прямим кутом, утворюючи ідеальну симетрію, яка нагадує хрест у серці форми. Це не випадково: така структура робить квадрат стійким, і архітектори часто використовують цей принцип у дизайні будівель, де діагоналі додають міцності конструкціям.
Переходячи до трикутників, діагоналей тут немає, бо всі вершини суміжні, але в багатокутниках з більшою кількістю сторін вони множаться. У п’ятикутнику, скажімо, п’ять діагоналей утворюють зірку, яка надихала митців від Леонардо да Вінчі до сучасних графічних дизайнерів. Кожна така лінія несе в собі математичну магію, дозволяючи розрахувати площі чи кути з точністю, що дивує.
А в тривимірному просторі, як у кубі, діагоналі стають просторовими – вони пронизують об’єм, з’єднуючи вершини через грані. Уявіть кубик Рубіка: його просторова діагональ від одного кута до протилежного вимірює шлях через весь об’єм, і це ключ до розуміння об’ємних розрахунків у фізиці чи архітектурі. Такі діагоналі додають глибини, перетворюючи плоскі ідеї на об’ємні реальності, що пульсують життям.
Формули для розрахунку діагоналі в різних фігурах
Для прямокутника формула діагоналі базується на теоремі Піфагора: d = √(l² + w²), де l – довжина, w – ширина. Це ніби корінь з суми квадратів сторін, що вистрілює точне значення, корисне для телевізорів чи моніторів, де 55-дюймовий екран по діагоналі може мати сторони 48 на 27 дюймів. Такий розрахунок робить вибір техніки інтуїтивним, дозволяючи уявити реальний розмір без вимірювальної стрічки.
У ромбі діагоналі перетинаються під прямим кутом і ділять одна одну навпіл, з формулою для однієї: d1 = 2 * √( (s/2)² + (h/2)² ), де s – сторона, h – висота. Це створює ефект метелика, де діагоналі розкривають фігуру, і в ювелірній справі такі розрахунки допомагають створювати ідеально симетричні прикраси. А в паралелограмі формула ускладнюється: d = √(a² + b² + 2ab cosθ), враховуючи кут між сторонами, що додає динаміки.
Для багатокутників кількість діагоналей обчислюється як n(n-3)/2, де n – кількість вершин. У восьмикутнику це дає 20 діагоналей, утворюючи складну мережу, яка нагадує павутину – ідеальний приклад для вивчення графів у комп’ютерних науках. Ці формули не сухі рівняння, а живі інструменти, що оживають у руках інженера чи дизайнера.
Застосування діагоналі в математиці та повсякденному житті
У матрицях головна діагональ – це лінія елементів від лівого верхнього кута до правого нижнього, де в одиничній матриці стоять одиниці, а решта – нулі. Це серце матриці, що визначає її властивості, як детермінант чи власні значення, і в програмуванні такі діагоналі оптимізують алгоритми для швидких обчислень. Подумайте про Excel: діагональ у таблиці даних може виділити ключові тренди, роблячи аналіз даних емоційно насиченим відкриттям.
У повсякденному житті діагональ з’являється в архітектурі – у Ейфелевій вежі діагональні балки забезпечують стійкість, розподіляючи навантаження з грацією танцюриста. У спорті, як у футболі, діагональний пас через поле змінює хід гри, додаючи несподіванки. А в дизайні інтер’єрів діагональне розміщення меблів візуально розширює простір, ніби розсуваючи стіни чарівним чином.
Сучасні технології підносять діагональ на новий рівень: у смартфонах вона визначає розмір екрану, впливаючи на комфорт перегляду. За даними виробників, як Samsung, екрани з діагоналлю 6.5 дюймів стали стандартом для 2025 року, балансуючи між портативністю та функціональністю. Це не просто число – це відчуття, коли екран оживає в руках, роблячи кожен дотик особливим.
Діагональ у мистецтві та культурі
У живописі діагональні лінії створюють динаміку, як у картинах Ван Гога, де вони передають рух вітру чи емоцій. Це ніби струмок, що тече через полотно, притягуючи погляд і додаючи глибини. У кіно діагональні кадри будують напругу, направляючи увагу глядача, як у фільмах Хічкока, де така композиція робить сцени незабутніми.
Культурно діагональ символізує перехід: у фен-шуй діагональні шляхи в саду приносять гармонію, з’єднуючи елементи. У літературі метафора діагоналі описує несподівані зв’язки, як у романах, де сюжет пронизує час. А в сучасній поп-культурі, від мемів до ігор, діагональ стає символом креативності, наприклад, у “The Legend of Zelda”, де діагональні рухи героя додають стратегії.
Історія терміну сягає античності: Евклід у “Елементах” описував діагоналі для доказів, впливаючи на Ренесанс. Сьогодні в цифровому мистецтві, як у NFT, діагональні патерни створюють унікальні твори, роблячи мистецтво доступним і динамічним.
Практичні приклади та розрахунки діагоналі
У будівництві діагональ перевіряє прямокутність рам: якщо діагоналі рами рівні, вона ідеальна. Для кімнати 4×3 метри діагональ – √(16+9) = 5 метрів, що допомагає в укладанні підлоги. Це практичний трюк, що економить час і додає впевненості в роботі.
У графіці діагональ у векторних зображеннях визначає роздільну здатність: для екрану 1920×1080 пікселів діагональ у пікселях – √(1920² + 1080²) ≈ 2203, що впливає на чіткість. У фотографії діагональний композиційний прийом “золотий перетин” робить знімки живими, ніби вони дихають.
У фізиці діагональ у векторах представляє результуючу силу: якщо дві сили діють під кутом, їх діагональ дає сумарний ефект. Це пояснює, чому мости з діагональними опорами витримують бурі, додаючи історії про інженерні дива.
Ось порівняльна таблиця формул для діагоналей у поширених фігурах, щоб полегшити розуміння відмінностей.
| Фігура | Формула діагоналі | Приклад |
|---|---|---|
| Квадрат (сторона a) | d = a√2 | Для a=5: d≈7.07 |
| Прямокутник (l, w) | d = √(l² + w²) | l=4, w=3: d=5 |
| Ромб (сторона s, кут θ) | d1 = 2s sin(θ/2) | s=2, θ=60°: d1≈1.73 |
| Куб (ребро a) | d = a√3 | a=1: d≈1.73 |
Ці формули взяті з математичних джерел та підручників з геометрії. Вони показують, як діагональ адаптується до форми, роблячи розрахунки універсальними. У реальному житті така таблиця допомагає швидко перевірити проєкти, додаючи впевненості в точності.
Історія та еволюція поняття діагоналі
Античні греки, як Піфагор, відкрили властивості діагоналі в квадраті, довівши ірраціональність √2, що потрясло світ математики. Це відкриття, ніби блискавка, розкололо уявлення про числа, впливаючи на філософію. У середньовіччі Аль-Хорезмі розвинув ідеї в алгебрі, де діагоналі матриць стали основою для рівнянь.
У Ренесансі Леонардо да Вінчі використав діагоналі в “Вітрувіанській людині”, символізуючи гармонію тіла. Сьогодні в комп’ютерній томографії діагональні зрізи створюють 3D-зображення, рятуючи життя. Ця еволюція робить діагональ живою істотою, що росте з людським прогресом.
У 2025 році, з розвитком VR, діагоналі в віртуальних світах оптимізують графіку, роблячи ігри immersивними. Це не кінець історії – діагональ продовжує еволюціонувати, надихаючи на нові відкриття.
Цікаві факти про діагональ
- 🔍 У шахах діагональний рух слона дозволяє контролювати до 13 клітинок на дошці, роблячи його потужною фігурою в стратегії – це чиста геометрія в грі!
- 🌟 Діагональ Золотого перетину в прямокутнику надихнула архітектуру Парфенона, де пропорції створюють ілюзію досконалості, що досі зачаровує туристів.
- 📱 Розмір телевізійних екранів завжди вимірюється по діагоналі, бо це дає ілюзію більшого розміру – трюк маркетологів, що працює з 1930-х років.
- 🧮 У теорії множин Кантор довів, що діагональний аргумент показує нескінченність реальних чисел, революціонізуючи математику в 19 столітті.
- 🎨 У оптичному мистецтві, як у роботах Васарелі, діагоналі створюють ілюзії руху, обманюючи око і роблячи картини живими.
Ці факти підкреслюють, як діагональ переплітається з життям, додаючи шарів до її простого визначення. Вони роблять тему не сухою, а повною відкриттів, що спонукають до подальших роздумів.
Сучасні виклики та інновації з діагоналями
У урбаністиці діагональні пішохідні шляхи в містах, як у Барселоні, скорочують час подорожі, роблячи мегаполіси зручнішими. Але виклики виникають у цифровій безпеці: діагональні атаки в кіберпросторі, як у матрицях даних, вимагають нових алгоритмів захисту. Інновації, як у 3D-друку, використовують діагональні шари для міцності об’єктів.
У освіті інтерактивні додатки, як GeoGebra, дозволяють візуалізувати діагоналі, роблячи уроки захоплюючими для дітей. А в екології діагональні вітрові ферми оптимізують енергію, зменшуючи вплив на природу. Ці приклади показують, як діагональ адаптується до сучасних проблем, стаючи частиною рішень.
Ви не повірите, але в моді діагональні шви в одязі додають елегантності, як у сукнях Діора, де вони підкреслюють фігуру. Це універсальність, що робить діагональ вічним елементом творчості.