Гострий трикутний дах над хатою відганяє дощ, а поле у формі трикутника вабить фермера свіжим урожаєм. Ця проста геометрична фігура ховає в собі безліч секретів, і обчислення її площі — ключ до багатьох практичних задач. Знаючи довжину однієї сторони та висоту до неї, ви миттєво перетворюєте абстрактні цифри на реальну територію, готову до використання.
Трикутник завжди привертає увагу своєю стабільністю — три точки визначають площину, а його форми варіюються від гострокутних шпилів соборів до розслаблених обрисів гірського схилу. Основна ідея полягає в тому, щоб розбити фігуру на знайомі частини, як-от прямокутник чи паралелограм. Саме так народилася перша формула, яка працює для будь-якого трикутника, незалежно від того, чи він рівний, чи нерівний.
Базова формула: половина добутку основи на висоту
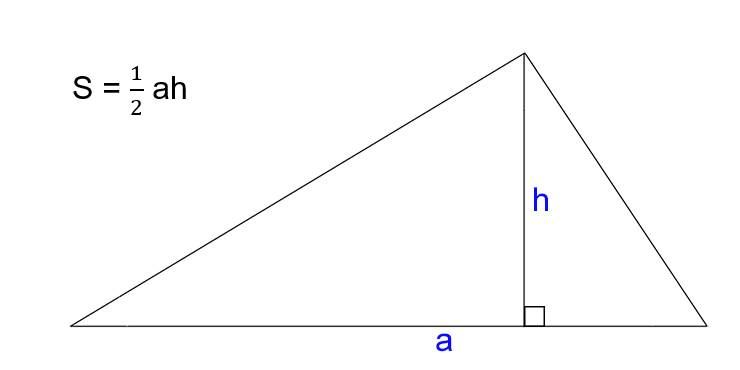
Найпростіший спосіб нагадує розрізання паралелограма навпіл — дві рівні частини дають площу трикутника. Формула звучить так: S = (1/2) × a × h, де a — довжина основи (будь-якої сторони), а h — висота, опущена перпендикулярно до цієї основи. Ця висота може падати всередину гострокутного трикутника або зовні тупокутного, але принцип незмінний.
Уявіть дах будинку: основа — карниз у 10 метрів, висота від карниза до вершини — 4 метри. Тоді площа одного схилу дорівнює (1/2) × 10 × 4 = 20 квадратних метрів. Легко, правда? А тепер подумайте про фермера, який планує посіви на трикутній ділянці — без цієї формули розрахунок зайняв би години з рулеткою.
- Виберіть основу — найзручнішу сторону для вимірювання.
- Виміряйте висоту перпендикулярно до основи, використовуючи рівень або теодоліт.
- Помножте і поділіть на два — результат готовий для використання в будівництві чи ландшафтному дизайні.
Цей метод ідеальний для початківців, бо не вимагає складних обчислень. Він лежить в основі багатьох програм для землемірів, де лазерний далекомір миттєво фіксує висоту. Пам’ятайте: висота повинна бути строго перпендикулярною, інакше результат спотвориться, як кривий дах під вітром.
Формула Герона: коли висоти немає під рукою
Три сторони — і площа готова, без зайвих вимірювань. Давньогрецький математик Герон Александрійський у I столітті н.е. відкрив цей скарб у своєму трактаті “Метрика”, дозволивши обчислювати площу будь-якого трикутника лише за довжинами сторін. Формула: S = √[p(p – a)(p – b)(p – c)], де p = (a + b + c)/2 — півпериметр.
Візьміть трикутник зі сторонами 5 см, 5 см і 6 см. Півпериметр p = (5+5+6)/2 = 8 см. Тоді S = √[8(8-5)(8-5)(8-6)] = √[8×3×3×2] = √144 = 12 см². Чарівно! Ця формула рятує в польових умовах, коли висоту виміряти важко, наприклад, на нерівній ділянці землі.
Доведення спирається на тригонометрію: площа також дорівнює (1/2)ab sin C, а теорема косинусів пов’язує сторони з кутом. Розклавши sin²C, виходить саме вираз під коренем. Джерело: uk.wikipedia.org (Формула Герона).
- Перевірте нерівність трикутника: a + b > c, інакше фігура неможлива.
- Обчислюйте послідовно: спочатку p, потім добуток, корінь — уникнете помилок у калькуляторі.
- Для великих сторін використовуйте комп’ютерні програми, бо ручні обчислення втомлюють.
Геронівська магія перетворює хаос вимірювань на точний результат, ніби алхімік з піску робить золото площі.
Площа через дві сторони та включений кут
Коли відомі дві сторони та кут між ними, формула оживає динамікою: S = (1/2) × a × b × sin C. Синус кута робить обчислення чутливим до форми — гострий кут дає малу площу, тупий — більшу, але менше 180°.
Приклад: сторони 7 м і 8 м, кут 60°. Sin 60° = √3/2 ≈ 0.866, S = (1/2)×7×8×0.866 ≈ 24.1 м². Ідеально для архітекторів, що проектують трикутні панелі з відомими кутами зварювання.
Цей метод сягає Евкліда, який у “Началах” заклав основи тригонометрії. Варіюйте кути для різних сценаріїв — від комп’ютерної графіки, де вершини моделі задаються з кутами, до GPS-навігації для розрахунку зон покриття.
Спеціальні трикутники: швидкі формули для знайомих форм
Рівносторонній трикутник сяє симетрією — всі сторони a, висота h = (a √3)/2. Площа: S = (a² √3)/4. Для a=10 см: S ≈ 43.3 см². Як мед з вулика, солодко і просто.
Рівнобедрений: основа b, бічні a, висота h = √(a² – (b/2)²). Площа стандартна, але з трюком для висоти. Прямокутний: S = (1/2) × катет1 × катет2, бо катети — основа і висота. 3-4-5: S=6.
| Тип трикутника | Формула | Приклад |
|---|---|---|
| Рівносторонній | S = (a² √3)/4 | a=4: S=6.928 |
| Прямокутний | S = (1/2)ab | a=5, b=12: S=30 |
| Рівнобедрений | S = (1/2)bh, h=√(a²-(b/2)²) | b=6, a=5: S=12 |
Джерела даних: uk.khanacademy.org та mathworld.wolfram.com.
Ці формули прискорюють задачі для школярів чи інженерів, де форми стандартні, як у мостах чи дахах.
Площа трикутника за координатами вершин
У цифрову еру вершини задають координатами (x1,y1), (x2,y2), (x3,y3). Формула Гаусса (шнурування): S = (1/2) |x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)|. Для точок (0,0), (4,0), (2,3): S = (1/2)|0(0-3)+4(3-0)+2(0-0)| = (1/2)|12| = 6.
Комп’ютерна графіка в Blender чи AutoCAD використовує це для 3D-моделей — трикутні сітки покривають поверхні. Землеміри з GPS вводять координати, і площа готова для кадастру.
Вектори: якщо AB і AC, S = (1/2) |AB × AC|. Простий детермінант ховає потужність лінійної алгебри.
Типові помилки 🚫
- ❌ Забули поділити на 2 у базовій формулі — виходить площа паралелограма, удвічі більша! Перевіряйте одиниці.
- ❌ У Герона не перевірили нерівність: 1+1>3? Ні, трикутника немає, корінь уявний. 😅
- ❌ Висота не перпендикулярна — похила лінія спотворює на 20-30%. Використовуйте рівень.
- ❌ У координатах забули модуль | | — площа не буває від’ємною, як борг у плюсі.
- ⚠️ Для тупокутного висота зовні — не ігноруйте, бо площа та ж, але інтуїція підводить.
Ці пастки підстерігають навіть досвідчених, але з практикою ви їх обійдете, як майстер обходить перешкоди на будові.
Площа в реальному світі: від пірамід до смартфонів
Єгиптяни будували піраміди, розбиваючи на трикутники для розрахунку каменю — площа бічної грані визначала об’єм піску для розрівнювання. Сьогодні в Україні землеміри на Полтавщині чи Київщині використовують дрони з координатами для трикутних полів, оптимізуючи посіви сої чи пшениці.
У графіці ігор як Cyberpunk 2077 мільйони трикутників формують світи — формула Гаусса обчислює текстури в реальному часі. Архітектори моделюють дахи соборів у Харкові, де sin C допомагає з кутами стропил. Навіть у фітнесі: площа трикутної зони на тілі для крему — практична дрібниця.
Спробуйте самі: намалюйте трикутник на карті вашого городу, застосуйте формулу — і ось план готов. Трикутник не просто фігура, а інструмент, що будує світ навколо.