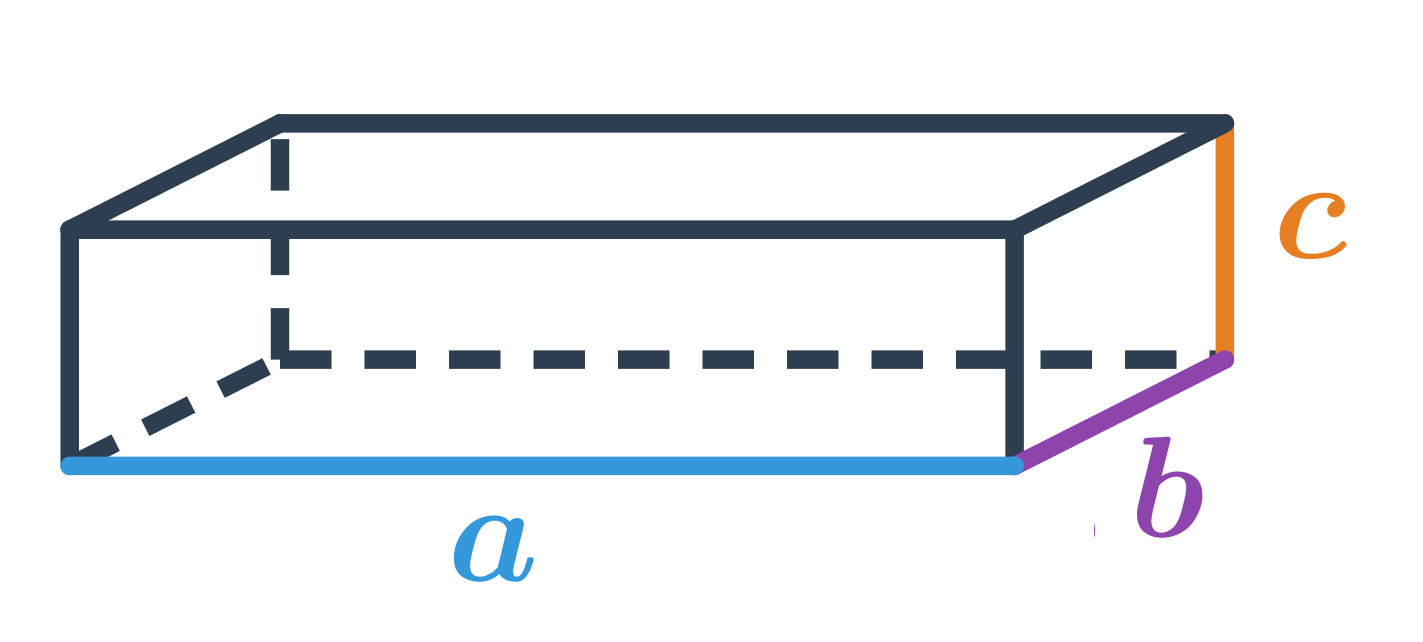
Паралелепіпед ховає в собі простір, ніби невидиму скарбницю, де кожна грань розповідає свою історію. Об’єм цієї тривимірної фігури з шістьма паралелограмними гранями дорівнює добутку площі основи на висоту, незалежно від того, чи стоїть він рівно, як коробка з-під взуття, чи нахиляється під хитрою кутом. Для прямокутного паралелепіпеда все зводиться до простого множення трьох вимірів: довжини, ширини та висоти – V = a × b × c. А от коли грані скошуються, на сцену виходять вектори, і об’єм оживає як модуль скалярного добутку трьох ребер від однієї вершини.
Ця формула працює як чарівний ключ, відчиняючи двері до точних розрахунків у школі чи на роботі інженера. Уявіть кімнату 4 м на 5 м з висотою 2,7 м – її об’єм миттєво 54 кубічних метри, готових вмістити меблі та спогади. Такий підхід рятує від плутанини, бо висота завжди перпендикулярна основі, а не дорівнює довжині ребра. Далі розберемося, як це працює на практиці, з цифрами та хитрощами.
Коли паралелепіпед витягується в космос векторів, об’єм набуває нового дихання: V = | \vec{a} \cdot (\vec{b} \times \vec{c}) |. Тут хрестовий добуток дає площу паралелограма з двох ребер, а скалярний множить на висоту третього. Згідно з uk.wikipedia.org, це фундаментальний спосіб для будь-якого паралелепіпеда, від прямого до найскладнішого похилого.
Що ховається за назвою: сутність паралелепіпеда
Паралелепіпед народжується з трьох пар паралельних граней, кожна з яких – паралелограм, що танцює в тривимірному просторі. Ця фігура нагадує призму з паралелограмною основою, де протилежні ребра рівні, а діагоналі перетинаються посередині, ділячись навпіл. Уявіть цеглину, яку трохи посунули збоку – ось і паралелепіпед у всій красі, стійкий і гнучкий водночас.
Його грані не просто плоскі; вони визначають простір усередині. Кожна пара граней паралельна, створюючи ефект нескінченної симетрії. Такі властивості роблять паралелепіпед основою для складніших структур, від кристалічних ґраток до 3D-моделей у комп’ютерних іграх. Без нього не обійтися в архітектурі чи фізиці, де об’єм – це не абстракція, а реальна місткість.
Види паралелепіпедів: від простого до витонченого
Паралелепіпедам не сидиться на місці – вони еволюціонують від найпростіших форм до хитрих конструкцій. Прямий паралелепіпед тримає бічні ребра вертикально, перпендикулярно основі, роблячи чотири грані прямокутниками. Прямокутний – це його досконала версія, де всі кути прямі, а грані – прямокутники чистої води.
Куб вирізняється особливою симетрією: всі ребра рівні, грані – квадрати. А похилий паралелепіпед грає на кутах, скошуючи бічні ребра, що робить його об’єм меншим за видиме на перший погляд. Ромбічний варіант склеює всі ребра в одну довжину, утворюючи ромбоедр – ідеал для кристалів. Кожен тип несе унікальний характер, але об’єм у всіх підкоряється єдиній логіці.
Щоб краще розібратися, ось таблиця порівняння ключових рис:
| Тип паралелепіпеда | Грані | Формула об’єму | Приклад з життя |
|---|---|---|---|
| Прямокутний | Всі прямокутники | V = a × b × c | Кімната, коробка |
| Прямий | Основа – паралелограм, бічні – прямокутники | V = S_осн × h | Контейнер з трапецієподібною основою |
| Похилий (загальний) | Всі паралелограми | V = | \vec{a} \cdot (\vec{b} \times \vec{c}) | | Кристал у мінералі |
| Куб | Квадрати | V = a³ | Кістка доміно |
Таблиця базується на стандартних геометричних визначеннях з uk.wikipedia.org. Вона показує, як простота переходить у складність, але об’єм завжди тримається за площу та висоту. Тепер розберемо кожну формулу по кісточках.
Об’єм прямокутного паралелепіпеда: найпростіший старт
Прямокутний паралелепіпед – улюбленець шкільних задач, бо його об’єм виходить одним помноженням. Візьмімо кімнату: довжина 6 м, ширина 4 м, висота 2,5 м. V = 6 × 4 × 2,5 = 60 м³. Це об’єм повітря, яке наповнює простір, або води в басейні такої форми. Легко? Але ключ – у точних вимірах, бо помилка на сантиметр множить кубами.
Формула V = a × b × c універсальна для будь-яких одиниць: см³ для маленьких коробок, л для акваріумів (1 л = 0,001 м³). Уявіть акваріум 50 см × 30 см × 40 см: V = 50 × 30 × 40 = 60 000 см³ = 60 л. Риби в захваті! А для куба все ще простіше: сторона 3 см дає 27 см³, ніби маленька крижана бричка.
- Виміряйте три ребра від кута: довжину, ширину, висоту.
- Перемножте їх безпосередньо – висота тут уже перпендикулярна.
- Перевірте одиниці: м × м × м = м³.
Такий підхід ідеальний для початківців, бо не вимагає зайвих кроків. Але переходьмо до складніших братів, де основа вже не прямокутник.
Прямий паралелепіпед: гра з площею основи
Тут основа – паралелограм, а бічні ребра стирчать вертикально. Об’єм лишається V = S_осн × h, де S_осн рахується як добуток сторони на висоту паралелограма чи | \vec{a} \times \vec{b} |. Візьмімо основу з сторонами 5 см і 4 см під кутом 60°: висота паралелограма 4 × sin(60°) ≈ 3,464 см, S_осн ≈ 17,32 см². З висотою h=10 см виходить V ≈ 173,2 см³.
Практика оживає в контейнерах: уявіть ящик з ромбоподібною основою для фруктів. Площа основи множиться на висоту штабеля – і ось об’єм урожаю на долоні. Цей метод нагадує, як геометрія служить логістиці, оптимізуючи простір.
- Знайдіть площу основи: для паралелограма base × height_парал або ab sinθ.
- Виміряйте перпендикулярну висоту до основи.
- Помножте – готово!
Плавний перехід до загального випадку показує, що навіть скошені форми не лякають, якщо знати інструменти.
Загальний паралелепіпед: векторна магія об’єму
Тут сяє справжня краса: три вектори \vec{a}, \vec{b}, \vec{c} від вершини задають весь паралелепіпед. Об’єм – абсолютне значення детермінанта матриці з їх координатами або скалярного добутку. V = \left| \det \begin{pmatrix} a_x & a_y & a_z \\ b_x & b_y & b_z \\ c_x & c_y & c_z \end{pmatrix} \right|. Це як код геному фігури – компактний і потужний.
Приклад: \vec{a} = (3,0,0), \vec{b} = (0,4,0), \vec{c} = (1,1,2). Детермінант: 3(4·2 – 0·1) – 0 + 0 = 3×8 = 24. V=24 одиниць. А якщо скосимо: \vec{c}=(1,1,5), det=3(4·5-0·1)-0+0=60, об’єм зріс! У комп’ютерній графіці це рятує для рендерингу об’ємів моделей, де кути божеволіють.
Ще один кейс з координатами: вершини A(0,0,0), B(2,1,0), D(1,0,3), C=B+(D-A)=(3,1,3). Вектори AB=(2,1,0), AD=(1,0,3), AC? Ні, для об’єму AB, AD, висота. Детермінант з AB, AD, скажімо AE де E вершина. Легко обчислити онлайн чи калькулятором, але розуміння векторів робить вас королем простору.
Крок за кроком: координатний розрахунок
Задайте координати трьох векторів. Складіть матрицю. Обчисліть det = a_x(b_y c_z – b_z c_y) – a_y(…) + a_z(…). Візьміть |det|. Готово! Це працює для кристалів, де unit cell – паралелепіпед, і об’єм клітини визначає густину речовини.
Практичні кейси: паралелепіпед у реальному світі
Уявіть архітектора, що моделює скошений дах: паралелепіпедний блок дасть точний об’єм снігу чи утеплювача. У кристалографії 14 типів ґраток базуються на паралелепіпедах – від кубічних до ромбоедричних, де об’єм клітини рахується векторно для аналізу рентгенівських даних.
У геймдеві bounding box – прямокутний паралелепіпед для колізій, а для реалістичних об’єктів – загальний для об’ємного рендерингу. Навіть у логістиці: контейнери ISO часто скошені під навантаженням, і V=S×h рятує від перевантаження.
Ось список реальних застосувань:
- Будівництво: об’єм бетону в скошеній формі.
- Фізика: об’єм елементарної комірки в твердих тілах.
- Графіка: voxelization складних форм.
- Щоденне: акваріуми, ящики, кімнати.
Ці приклади перетворюють абстракцію на інструмент, що економить час і гроші.
Типові помилки при розрахунку об’єму паралелепіпеда
Багато хто плутає висоту з довжиною бічного ребра в похилому випадку – h завжди перпендикулярна! Результат завищується, як переповнена коробка. Ще пастка: забути модуль детермінанта, бо знак залежить від орієнтації векторів.
- Використання довжини ребра замість висоти: для кута 30° похибка до 15%.
- Ігнор одиниць: см × м = маячня, завжди переводьте.
- Компланарні вектори: det=0, об’єм нуль – фігура сплющується.
- Неправильна площа основи: sinθ, а не просто a×b.
Перевіряйте кроками: візуалізуйте, малюйте, тестуйте на відомому кубі. Це врятує від фрустрації та помилок у проектах.
Роблячи ці виправлення, розрахунки стають точними, як лазерний промінь. Паралелепіпед перестає бути загадкою, перетворюючись на союзника в творенні та обчисленні.
У комп’ютерних симуляціях об’єм паралелепіпеда моделює потоки в пористих середовищах, де кожна комірка – мініатюрний світ. А в дизайні меблів скошені форми додають стилю, але вимагають точного V для матеріалів. Геометрія пульсує життям, запрошуючи до нових експериментів з формами та числами.