Трикутник стоїть на основі, а висота тягнеться до неба, ніби невидимий стрижень, що тримає всю конструкцію. Найшвидший шлях до її обчислення лежить через площу: якщо знаєте S і довжину основи a, то висота h просто дорівнює h = 2S / a. Ця формула працює для будь-якого трикутника, незалежно від його форми – від гострокутного красеня до тупого важковага. А далі розберемо, як діяти, коли площі немає під рукою.
Уявіть, що ви архітектор, і дах будинку – це трикутник: без точної висоти розрахунок матеріалів перетвориться на лотерею. Розрахунок починається з вибору основи, до якої опускаємо перпендикуляр з протилежної вершини. Ця лінія може ховатися всередині, лежати на боці чи навіть вистрибувати назовні в тупокутних фігурах. Тепер зануримося глибше, щоб жоден куточок теми не залишився в тіні.
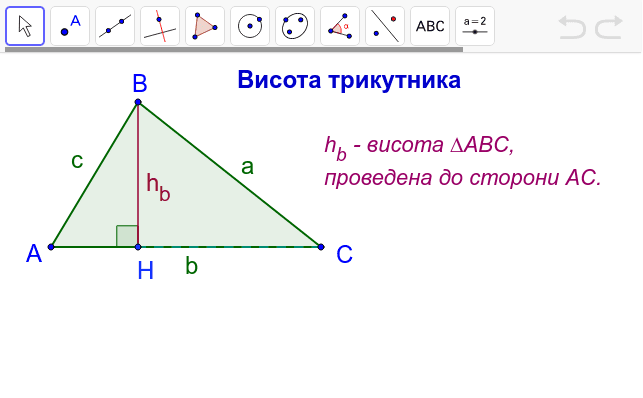
Що таке висота трикутника: основи, які варто запам’ятати
Висота – це перпендикулярний відрізок від вершини до лінії, що містить протилежну сторону. Не плутайте її з будь-якою довжиною: вона завжди 직각ова, як стрілка циркуля, що б’є точно в ціль. У гострокутному трикутнику всі три висоти затишно влаштовані всередині, ніби гості на затишній вечірці. У прямокутному дві з них збігаються з катетами, а третя пірнає до гіпотенузи. А в тупокутному одна висота вислизає за межі, нагадуючи втікача з балу.
Чому це важливо? Бо висота визначає площу: S = (1/2) * a * h. Звідси й універсальна формула, про яку згадали спочатку. За даними uk.wikipedia.org, найдовша висота завжди стоїть навпроти найкоротшої сторони – логічно, бо коротка основа вимагає більшої “підпори”. Три висоти сходяться в ортоцентрі, тій містичній точці, яка робить трикутник особливим. Без розуміння цього базису подальші розрахунки перетворяться на сліпе тиняння.
Практичний нюанс: висота не завжди падає на сторону – іноді на її продовження. Малюйте уважно, бо інакше помилитеся в знаках і отримаєте від’ємну величину, що смішно, але дратує.
Універсальна формула висоти через площу: ваш перший інструмент
Знаєте площу й основу? Забудьте про складнощі – h = 2S / a вирішує все миттєво. Площа може бути відома з вимірювань або розрахунків, але якщо ні, то вперед до Герона: спочатку обчисліть напівпериметр s = (a + b + c)/2, потім S = √[s(s-a)(s-b)(s-c)]. Тільки після цього h_a = 2S / a.
Приклад для новачків: трикутник з основою 10 см і площею 25 см². h = 2*25 / 10 = 5 см. Просто, як дважды два. А для перевірки візьміть сторони 3,4,5 (прямокутний): s=6, S=√[6(6-3)(6-4)(6-5)]=6, h до основи 5 = 2*6/5=2.4 см. Перевіряється!
Цей метод блискучий для будь-яких фігур, бо не залежить від кутів чи симетрії. У реальному житті інженери в AutoCAD вводять площу з лазерних сканерів і миттю отримують висоту для балок. Варіюйте основу – отримайте три різні висоти для одного трикутника, як різні ракурси фото.
Висота в прямокутному трикутнику: катети як союзники
Тут все спрощується до геніальності. Два катети – готові висоти до них самих, бо перпендикулярні. А висота до гіпотенузи c з вершини прямого кута вражає: h_c = (a * b) / c. Звідки? З подібності трикутників, що утворюються при опусканні.
Розберімо на пальцях: катети 3 і 4, гіпотенуза 5. h_c = 12/5 = 2.4 см, як у попередньому прикладі. Альтернатива через проекції: h_c = √(p * q), де p і q – сегменти гіпотенузи (p = a²/c, q=b²/c). Перевіряємо: p=9/5=1.8, q=16/5=3.2, √(1.8*3.2)=√5.76=2.4. Ідеально збігається.
У будівництві це золото: дах у формі прямокутного трикутника вимагає точної висоти для крокв. Помилка на сантиметр – і покрівля з’їде. Для просунутих: у координатах вершини (0,0), (a,0), (0,b) – висота до гіпотенузи легко через рівняння прямих.
Рівнобедрений трикутник: симетрія спрощує життя
Дві рівні сторони – і висота до основи стає медіаною та бісектрисою, розділяючи основу навпіл. Формула з Піфагора: якщо бічні a, основа b, то h = √(a² – (b/2)²). Ніби розколюєте трикутник на два дзеркальні прямокутні.
Приклад: основа 8 см, бічні 5 см. h = √(25 – 16) = √9 = 3 см. Тепер висота до бічної сторони: спочатку площа S=(1/2)*8*3=12, h_b = 2*12/5=4.8 см. Симетрія гарантує рівність двох таких висот.
У дизайні меблів чи флагах це незамінно – рівнобедрений трикутник всюди. Гумор: якщо b>2a, висота уявна, трикутник не існує. Перевіряйте нерівність трикутника перед розрахунком!
Рівносторонній трикутник: магія кореня з трійки
Всі сторони рівні – висоти теж. Формула: h = (√3 / 2) * a. Звідки? Розділіть на два прямокутні 30-60-90, де короткий катет a/2, протилежний 60° – (√3/2)a.
Приклади з mathros.net.ua: a=7, h≈6.062 см; a=9, h≈7.794 см. Площа S=(√3/4)a², звідки h=2S/a збігається. Для зворотного: a=2h/√3.
У графіці та ювелірці це хіт – ідеальна пропорція. Факт: у природі бджолиний стільник використовує шестикутники з рівносторонніми трикутниками для максимальної міцності.
Довільний трикутник: повний арсенал через Герона та сторони
Без симетрії – комбінуйте Герона з h=2S/a. Сторони 6,7,8: s=10.5, S=√[10.5(4.5)(3.5)(2.5)]≈21.27, h_a(до6)=2*21.27/6≈7.09 см.
Інша формула: h_a = (b c / (2 R)), де R – радіус описаного кола, R=abc/(4S). Складніше, але для просунутих. Або координатний метод: вершини A(x1,y1), B(x2,y2), C(x3,y3), h до BC через відстань від точки до лінії.
У топографії це рятує: виміряли сторони дроном – висоту маєте для карт.
Тригонометрія в грі: кути як ключі до висоти
З двома сторонами та кутом між: S=(1/2)bc sinA, h_a= b sinC = c sinB. Елегантно! Приклад: b=5, γ=30°, h_a=5*sin30°=2.5.
Закон синусів підсилює: a/sinA = 2R, звідки виводимо висоти. Для кодерів у Unity це must-have для 3D-моделей.
Ортоцентр і таємниці висот: для допитливих умів
Три висоти танцюють до ортоцентра – точки, де сходяться. У гострокутному – всередині, тупокутному – зовні, прямокутному – у вершині прямого кута. Властивість: h_a : h_b : h_c = 1/a : 1/b : 1/c.
За ua.onlinemschool.com, 1/h_a + 1/h_b + 1/h_c = 1/r. Ортоцентр пов’язаний з евлеровою лінією – міст до центроїда та оберненоцентра. У задачах НМТ це бомба для балів.
Типові помилки при пошуку висоти трикутника
Перша пастка: забуваєте, що в тупокутному висота зовні – берете модуль відстані. Друга: плутаєте основу з будь-якою стороною, бо висоти різні. Третя: для рівнобедреного забуваєте ділити основу навпіл, отримуєте √ від від’ємного.
- Ігнор перевірки трикутника: Якщо a+b ≤ c, фігура не існує – калькулятор видасть NaN, а ви в шоці.
- Неправильна площа: Помилка в Героні на 0.1 – і висота на сантиметри мимо. Завжди раундіть √3≈1.732.
- Координати без норми: Відстань до лінії ax+by+c=0 – |ax0+by0+c|/√(a²+b²), не забувайте знаменник.
Радість: калькулятори типу Desmos малюють висоти автоматом. Тренуйтеся на 10 задачах – і помилки зникнуть, як роса на сонці.
Таблиця формул: все в одному місці
Щоб не шукати по тексту, ось зведена таблиця ключових формул. Використовуйте для швидкого орієнтування, а нижче – розбір прикладів.
| Тип трикутника | Відомі дані | Формула висоти h_a (до сторони a) | Приклад |
|---|---|---|---|
| Довільний | S, a | h_a = 2S / a | S=20, a=8 → h=5 |
| Прямокутний | Катети b,c; гіпотенуза a | h_a = (b c)/a | 3-4-5 → h_5=12/5=2.4 |
| Рівнобедрений | Бічні b=c, основа a | h_a = √(b² – (a/2)²) | b=5, a=8 → h=3 |
| Рівносторонній | Сторона a | h = (√3 / 2) a | a=10 → h≈8.66 |
| Через Герона | Сторони a,b,c | S=√[s(s-a)(s-b)(s-c)], h_a=2S/a | 6-7-8 → h_6≈7.09 |
Таблиця базується на стандартних формулах з uk.wikipedia.org та ua.onlinemschool.com. Додайте свої приклади для практики – і тема ваша назавжди.
Практичні кейси: від шкільної зошита до інженерії
Кейс 1: Дах гаража – рівнобедрений з основою 6 м, бічними 4 м. h=√(16-9)=√7≈2.645 м. Скільки шиферу? Площа даху 2*(1/2*6*2.645)≈15.87 м².
Кейс 2: У грі Fortnite трикутникний щит з вершинами (0,0),(10,0),(5,8). Висота до основи [0-10] – просто y=8. До іншої сторони – рівняння лінії.
Кейс 3: Фізика – траєкторія снаряда утворює трикутник, висота = макс підйом. Розрахунок через v sinθ / g.
Останній штрих: у Photoshop для деформації фігур висота – ключ до пропорцій. Експериментуйте в GeoGebra – і математика оживе, як стара дружба.